That'll Go Over Like A Lead Balloon

Consider a lead-filled balloon...
By Jeff-perado

Everyone is familiar with the concept of buoyancy and that some gasses are “lighter than air.” Balloons filled with helium float, balloons blown up with normal air do not. Another method of creating a buoyant balloon is the hot air balloon. Air is heated up, it becomes buoyant and rises, fill a large enough balloon with hot air and it can carry a person of a group of people. How much weight a balloon can support depends on the size of the balloon and the temperature of the hot air.

The physics behind this phenomenon are quite interesting and can be used to show some highly unusual effects. Consider for a moment a balloon filled with lead vapor – would it float or crash to the ground? Using this scenario as a thought experiment can demonstrate the power of some basic physical principles, namely Archimedes’ principle of buoyancy, the ideal gas law, the concept of density, and Avagadro’s number.

First let’s look at the basic equations of buoyancy and how they relate to a balloon. We will consider the problem of trying to determine how big a balloon we would need if we wanted to lift a 100 Kg mass. The balloon will be helium filled.
We will assume:
The density of helium, ρ_H = 0.1787 Kg/m³
The density of the air (displaced by the balloon), ρ_A = 1.29 Kg/m³

What we want to know is the volume of the balloon (assume a spherical balloon), V = ?
The supported weight will be referred to as the payload mass, M = 100 Kg.

The buoyant force equation is:

[1]


Rearranging this we get:

[2]




The volume of the balloon needed to lift a 100 Kg payload using helium as the gas is:

.



Using the equation for a sphere we can find the radius of the balloon and hence the diameter:





Rearranging:

is the radius.

The diameter of the balloon is then: D = 5.56 m

Interestingly, determining how many smaller balloons it would take to replace the one large balloon can be done by using this relation:



Solving for N:



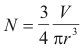
Assuming that we want to use balloons which are cheap and easily available, we will use a diameter of 2 feet for our balloons. This diameter translates to a radius of r = 0.3048 m.

Inserting this radius and the above determined volume into the equation we find that we need 759 balloons of a 2 foot diameter to replace the single balloon.

Examining the lead balloon problem:

We want to know if we can fill a balloon with a lead vapor and create a buoyant force. To perform this analysis, we will consider the same payload as the above example (M = 100 Kg). Also we will return to equation [2] of the buoyant force. To perform the calculation for lead vapor a few substitutions and rearrangements will need to be made:



For clarity, we will substitute ρ_Pb for ρ_g.

Since we do not know the density of lead vapor, we will have to calculate it. First we know from the definition of density that:

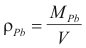[3]

Where M_Pb is the mass of the lead.in Kg, and V is the volume in m³.
Inserting this into the equation and using some algebraic manipulation:



[4]

Next we need to look at another physical principle, the ideal gas law. The ideal gas law describes the relationship between the amount of the gas and its temperature, pressure and volume. It should be pointed out that a balloon must have the same internal pressure as the external pressure of the air, or else the balloon would be either expanding or collapsing. The ideal gas law is represented by:

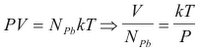[5]

Where:
N_Pb is the number of lead atoms in the vapor
k is the Boltzmann constant (= 1.381 x 10^-23 J/K)
T is the temperature of the gas (in K)
P is the pressure of the gas

Substituting in equation [4] and rearranging:

[6]

For simplification, let:


Also, the mass of an element and the number of atoms in the mass is related by Avagadro’s number, N_A:

[7]

Where:
W_Pb is the atomic weight of lead (= 0.2072 Kg/mol)
N_A is Avagadro’s number (= 6.022 x 10²³ atoms/mol)

Substituting these into [6]:



Again for simplification, let:




Solving for N_Pb and substituting:

[8] (The Stutz Equation)

This equation says that the ratio of the number of gas atoms in the balloon to the payload mass is equal to a constant (at a specified constant temp and pressure). It is important to note that this equation only holds true if the gas in question obeys the ideal gas law -- even in this rather exotic application, it is useful to point out that the Ideal Gas Law is still a very good approximation.

Also the two values, κ and ξ have special meanings. κ is the thermal mass reduction value and is based only on the thermodynamic properties of the buoyant gas. ξ is the material mass reduction value and is based only on the elemental properties of the buoyant gas.

Now lets look at flying our lead balloon. First we need the properties of lead. The boiling temperature of lead, T_B, is 2023K. The atomic weight, W_Pb, of lead is 0.2072 Kg/mol. Also let us assume that the pressure of the buoyant gas (and the atmosphere) is 1 atmosphere. That is
P = 1 atm = 1.10 x 10⁵ N/m². We will use the same payload mass, M = 100 Kg, and air density, ρ_A = 1.29 kg/m³.

The number of lead atoms is then:



Where:
The thermal mass reduction parameter is:



And the material mass reduction parameter is:



Plugging the value found for the number of lead atoms, N_Pb, back into equation [7]:



Thus heating lead to its boiling point of 2023K, it would take 2,164 Kg of lead to lift a payload of 100 Kg. Also the volume of this lead vapor balloon can be calculated from [4]:



And the density of the lead vapor is:



The only parameter we can change to reduce the mass and volume of the lead vapor is the temperature of the vapor. So let us consider changing the temperature to 2500K:


This affects the thermal mass reduction:



The number of lead atoms is then:



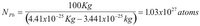
The mass of lead can again be found with equation [7]:



Again the volume of the balloon is calculated from [4]:



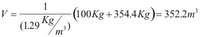
And the density of the lead vapor is:



Returning to the equation for a sphere:



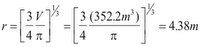
The diameter of the balloon is then: D = 8.76 m

Thus to change gasses from helium to lead vapor, the diameter of the balloon would only grow by about 3 meters (with the lead vapor at a temperature of 2500K).

Fun Facts:
We discovered to lift a weight of given mass, the mass of the lead needed would have to be greater.
We can turn any metal into a "lighter than air" vapor and create a bouyant force with it, no matter how heavy (or more precisely dense) the metal is.
Its a fun mental excercise, but heating lead to that temperature, 2023 K (3182 F), is very impractical, and would burn up any ballon material, making it unworkable in practice. Did I mention that it is very hot?

Conclusion:
The value of this mental exercise is the concept of mass reduction. Mass reduction is broken into two types, thermal mass reduction and material mass reduction. The thermal mass reduction is independent of the gas type, and only deals with the state of the gas. The material mass reduction only deals with the isotope or molecule properties. It is a function of the atomic/molecular weight of the gas alone. Thus any material that can be vaporized or exists as a gas can be put into this equation, taking into account how well it fits the ideal gas law. All that needs to be known about the material is its temperature and atomic/molecular weight.